MCMC lecture

http://videolectures.net/mlss09uk_murray_mcmc/

Last class

Our last class meeting will be Monday, June 4. If this interferes with your finals schedule, its fine to skip. But we will cover MCMC in a bit more detail, so if you'd like to learn, please show up!

Wrapping things up

We're closing in on the end of the term. Here's what's due and when:

• CA5 due Monday, June 4 (Dropbox) 
• Final projects due Friday June 8 (Dropbox)

Add this to the end of CA5:

8) Simulate a 5-pixel data set with flux per pixel described by F(z) = a*(z-1)^2 + b*(z-1) + c, with a=3, b=0.2, c=4. Then use an MCMC routine to produce the two-dimensional PDF for {a,b,c}, as well as the individual 1-dimensional PDFs for a, b and c. 


The basic algorithm for MCMC is as follows:

1. Evaluate the likelihood of the data at an initial, guessed set of parameters {a,b,c}. Call this L0
2. Evaluate a new likelihood L1 at a new set of parameters, say {a+delta,b,c}, where delta is a small perturbation drawn from a "jump distribution." This jump is usually just a call to a normally-distributed random number generator centered on the current value. The parameter to perturb is also drawn at random (there are other ways to do this, but this is the easiest in my experience).
3. If L1/L0 > 1, then add the new set of parameters to the chain (array of parameters). If L1/L0 < 1, then add the new parameters to the chain if a uniform random number is less than L1/L0. Else, just add the previous set of parameters to the chain.
4. Goto 1 until the desired number of chain links is calculated (usually 1e5 to 1e7 links).

For three parameters, the array of chains will be a 3xN array, where N is the number of chains run. Each chain turns out to be the marginalized, posterior pdf of that parameter, which is pretty cool.

For more info, check out Wikipedia, or Appendix A of this classic astronomy article:

http://arxiv.org/pdf/astro-ph/0310723v2.pdf

I will be available during office hours Wednesday (10am-11am) to go over MCMC in greater detail.

Drawing randomn Poisson numbers

How-to here.

Correction on my last post

Both the title and body of my previous post referenced Class Activity 2, when I meant to refer to Class Activity 4 (CA4). Since you already turned in CA2, I hope this wasn't too confusing!

Class Activity 4

For those of you who have completed CA4 through problem 2, you can consider yourselves complete on that class activity and you may turn in what you have. For those of you who completed through problem 4, kudos to you and you should feel good about the extra skills you picked up as a result. The time invested will pay off in your research career, I can assure you.

For now, I'd like all of you to focus on the reading assignment (Chapter 4.1 in Sivia) described in a previous post so you can get the most out of CA5 this Friday. I'll be back in town and I'll give a short lecture before we dive into the next activity.

2D posterior plot is easy ---CA3_problem4

Debugging is annoying and we frequently run into a lot of problems when plotting 2D posterior contour.  Believe me, you are not alone.  There is a simple code I used for CA3 problem4. It is not optimized but it shows some standard steps to do the 2D posterior plots which I find useful.

# step1: read your data and do some basic check (visualization is important)
# step2: prepare a 2D -parameter mesh grid, which can be done by meshgrid function in numpy
# step3: Given the 2D parameter grid, we can calculate the probability of each datum at the every grid    coordinate, i.e. , a 2D probability for each data point. It is usually convenient to do it in log scale.
# step4:  sum the log probability of all data points, then we have the joint 2D log probability for
 the whole data set.
# step5: find the maximum joint log probability and subtract it. We do this to avoid numerical outflow problem since unnormalized  joint probability is usually a very small value.
# step6: exp(log prob) and plot a contour

The example of CA3_problem4

from numpy import *
import math
import matplotlib
import matplotlib.pyplot as plt
import asciitable
import scipy

# read the data
data      = asciitable.read('fv05_vf05_data.txt')
detection = data['comp'] #detection or not 1/0
feh       = data['metallicity'] #metallicity

# check data

n         = detection.size    #the total number of data point
print feh.min(),feh.max()     # metallicity range in the data

#choose the proper range of alpha, f>0 --> alpha>0
alpha_grid= arange(0.01,0.1,0.001)
beta_grid = arange(.0,3.0,0.01)

# generate a 2D meshgrid for alpha and beta
(alpha,beta) = meshgrid(alpha_grid,beta_grid)
logpdf = zeros((beta_grid.size,alpha_grid.size))

# loop through each data point
for i in range(n):
    f = alpha*10**(beta*feh[i])
   
    f[(f >1)] = None
    #set f to none if f>1, here we don't need to check f>0
    # because we already set alpha>0
   
    # sum the log(prob) of the all data
    logpdf += log(detection[i]*f+(1-detection[i])*(1.-f))

# set the log(prob) at forbidden (alpha,beta) value to -999   
whereAreNaNs = isnan(logpdf)
logpdf[whereAreNaNs] = -999

# find the max logpdf
print logpdf.max()

# find the peak location

ind = where(logpdf == logpdf.max())

print 'the peak is at alpha=%.4f,beta=%.4f' %(alpha_grid[ind[1]],beta_grid[ind[0]]) 

logpdf = logpdf-logpdf.max()

# pdf is the normal probability function
pdf = exp(logpdf)

# 2D plot

plt.figure()
CS = plt.contour(alpha,beta,pdf)

New Reading

The reading assignment for this week is Sivia chapter 4.1 and the first subsection of 4.2 (up to 4.2.1).

Also, check out this post from last year on the Jeffreys' prior for a scale parameter, such as the slope of a linear fit. If you're feeling super inspired, check out  this dense yet handy Wikipedia entry.

Avoiding Loops: a homework example

In previous post, Tim has shown us that using array is much efficient than loops. Here I'm going to give a real example about how to use numpy array to solve one of our homework problem.

The example is CA4, problem3. We have a data set of the masses of known transit planets and want to find the power index of the mass distribution function.


##########################################################

from numpy import *
import asciitable
import pylab as py

# read the transit data
all_transits = asciitable.read('transits.csv',delimiter=",")
transit_mass = all_transits['MSINI']   

# find the data with 1 < m <20
ind = ((transit_mass >= 1)& (transit_mass <=20)).nonzero()[0]
mass_data = transit_mass[ind]

n =  mass_data.size  

# the total number of planets in the given mass range

# build an array for a possible alpha range
alpha_grid = arange(1.1,3.5,0.001)

# here we use numpy array rather than loop
# (1) we build 2D meshgrid arrays for alpha and mass
# NumPy provides a convenient function for generating meshgrid arrays,
# called, appropriately, meshgrid.

(alpha,mass) = meshgrid(alpha_grid,mass_data)
#print alpha
#print mass

#(2) Calculate the probability at each alpha and m
# Attention: array math operates on an element by element basis,
# i. .e, unlike matrix math.
mass_max =  mass_data.max()
mass_min = mass_data.min()
const = 1./(1-alpha)*(mass_max**(1.-alpha)-mass_min**(1.-alpha))
log_pdf = log(1./const*mass**(-1.*alpha))

# (3) we sum the log_pdf in the mass dimension
log_pdf_alpha = log_pdf.sum(axis = 0)
plot(alpha_grid,exp(log_pdf_alpha-log_pdf_alpha.max()))

##########################################################

The example code and transit planet data can be downloaded from here:

I find this introduction of numpy calculation very useful. It is totally worth your time.

http://www.physics.nmt.edu/~raymond/software/python_notes/paper003.html

CA3 data

Part 6 of CA3 instructs you to construct a data table based on FV05. In the interest of time and uniformity, you should just use this table instead:

http://www.astro.caltech.edu/%7Ejohnjohn/astrostats/data/fv05_vf05_data.txt

The middle column indicates 0 if the star doesn't have a planet, and 1 if it does.

Parts 1-8 will be due Monday. Continue on to problems 9 if you feel particularly inspired to learn about how to deal with measurement uncertainties when doing this sort of analysis. 

Part 10 instructs you to write up your results. This is left over from last year. This year I've already encouraged you to make your results clear, either in an iPython workbook or better yet a LaTeX document. You may turn in your completed activity the same way you did with CA1 and CA2.

Class Activity 3

http://www.astro.caltech.edu/~johnjohn//astrostats/CA3.pdf

Dispositive Nulls and Detection Limits

My good friend Prof. Jason Wright has been tackling the notion of a "dispositive null" over on his professional blog. Here's his first entry, and his followup. This is good stuff and a natural extension of the notion of assigning confidence to our belief in a hypothesis.

avoid using loops!

So one of the important things to know about python is that it is an "interpreted" language, not a compiled language.  Interpreted languages (like python, IDL, and Matlab) are designed to be "higher-level" languages, and thus do not have to be compiled in the same way as C or C++, for example.  This makes some things simpler, but there are some costs.

One of the costs is that loops take a long time to execute.  See the following example:

As you see, doing operations element-by-element on an array is MUCH slower than working with whole arrays at a time.  In fact, behind the scenes, numpy is using all the power of compiled code to make these array operations lightening-fast.  But you don't need to know how this works; all you need to do is get comfortable working with whole arrays, whenever possible.  A good example of this in action is the difference between the following two ways to create arrays of random numbers:

CA1 Solution Sets

Everyone did a nice job on the Class Activities this week. Thank you for all your hard effort and careful work. Coco has placed marked-up PDF files in all of your Dropbox folders. Here are three writeups that I feel constitute the "solution set."

Solution 1 (Peter)
Solution 2 (Melodie)
Solution 3 (Adam)

In the future, please strive to have your write-up be clear enough to serve as the solution set. Science is all about communication, so the clarity of your presentation is a big part of your assessment in this class.

arbitrary precision in Python

Some of you mentioned about the rounding error in python. There is a Python package which can give you arbitrary precision. Take a look if you are interested.

http://code.google.com/p/mpmath/

On Python Functionality

"Any self-respecting programming language has a histogram function!" -Jennifer

"Oh! Here it is!" -Jessica

Yikes!

IDL users: Be careful of the indexing of rows and columns in Python. From Jon Swift:

i.e. why has no one ever told me?
IDL:------IDL> a = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]]IDL> help,aA               INT       = Array[3, 4]

python:----------In [2]: a = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]]
In [3]: print np.shape(a)(4, 3)

Take the survey

Up there, at the top of the page. Click an answer. Feel good that your response will matter.

IDL to Python translation guide

https://www.cfa.harvard.edu/~jbattat/computer/python/science/idl-numpy.html

Office Hours w/ the Prof

In addition to the Wed night help sessions with Coco, I will also hold office hours from 10am-11:30am Wednesday mornings.

This!

Can any of you do this for Bayesian statistics, for e.g. line fitting? If you can and do, you get an A+, automatically.

DeTeXify

http://detexify.kirelabs.org/classify.html

hat tip: Iryna

CA1 modification

Based on feedback from Wednesday night's help session, it looks like I underestimated the time necessary to complete the class activity (in true professorial fashion). I forgot that problems 6 and 7 required derivations and that many of you have yet to learn LaTeX, and that problem 8 is nontrivial.

Here's the new plan:

Turn in problems 1-5 at the beginning of class Friday. We'll then spend Friday's class talking about LaTeX and working on fitting lines.

Handy LaTeX References

Learning how to write in LaTeX is a valuable skill to learn early in your scientific career. Don't be that guy/gal who writes their papers in Word. Ugh!

LaTeX Math Symbols:

http://web.ift.uib.no/Teori/KURS/WRK/TeX/symALL.html

Handy online LaTeX editor (click buttons for examples of code):

http://www.codecogs.com/latex/eqneditor.php

(also, check the URLs for all of the equations in the previous post for the LaTeX used to create them). 

How to pronounce and write "LaTeX":

http://en.wikipedia.org/wiki/LaTeX#Pronouncing_and_writing_.22LaTeX.22

I prefer "lay-tech" but I won't make fun of you if you say "lah-tech." I will make fun of you if you say "lay-teks" :)

Integrating exponentials

Often in physics, and sometimes in life, you come across the need to integrate an exponential of the form



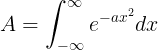
Allow me to show you how to handle this using simple dimensional analysis rather than calculus and memorization. Dimensional analysis can get you out of a bind when working on a plane (sans wireless), in an oral exam or even during Q&A after your colloquium!

First, note that the units of A must be the same as the units of x since exponentials are dimensionless and dx has units of x. Further, examination of the quantity in the exponent reveals that a must have units of 1/x^2, since the argument of an exponential must be dimensionless, too. Thus, the integral must have units of x and involve a, like so:



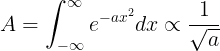
This is most of the way there. It turns out that there's a missing factor of the square-root of pi:



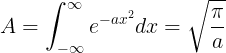
But I think it's pretty cool that you can get to within a factor of root-pi (1.77) without any calculus! I can pretty easily remember the pi part after I get the dimensions correct. Even if I forget, being within a factor of two is good enough for astronomy in most applications.

You might notice that this is the form of the Gaussian function, centered on x=0 with



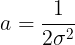
Once normalized, the Gaussian function becomes the normal distribution so frequently used in data analysis (and CA1). Note the distinction between a Gaussian function and a normal distribution. The difference is important, but frequently ignored in the scientific literature. For example, a Gaussian has three free parameters. A normal distribution has only two. And only one of these is a proper probability distribution function (pdf).

For more "Street Fighting Mathematics" like this, check out this book.

Normalization

I'm sorry I wasn't able to be there in class today. However, Coco reports that you all made good progress working on Class Activity 1. She also reports that many of you struggled with the normalization part of Problem (4). Assuming this is where the problem was, allow me to help everyone along.

Problem (4) states:

Without properly normalizing things, you will end up with a proportionality of the form:

In order for this to be an equation, you have to normalize it. You might want to convince yourself that the quantity on the right hand side is not normalized by integrating over all values of \mu. In fact, dividing by this integrated quantity provides the normalization constant:

The denominator is also known as the "evidence":



or the probability of the data given the model, with \mu marginalized out.

The actual value of the integral can be expressed analytically, or you could just do it numerically. Or you can use WolframAlpha. But whatever you do, don't get too hung up on this! :)

Ay117: Starting anew in 2012

Welcome to the new class of AstroStats students!

The (rough) course syllabus can be found here:

http://www.astro.caltech.edu/~johnjohn/astrostats/

I'll update this syllabus soon, but all of the key points that I covered in the first class today are there.

The first Class Activity is also available. I will post the activities on the right hand side of this blog throughout the term. We'll work on this activity starting Friday morning, and we'll continue through next week. Whatever we don't finish by the end of class Monday will be homework due Friday, unless otherwise specified.

The reading assignment is Chapters 1 and 2 of Sivia (link to Google Books). Once you finish Chapter 2, keep going. The standing reading assignment is all of Part I, to be completed before week 3 of class. Once you read Part I, read it again.